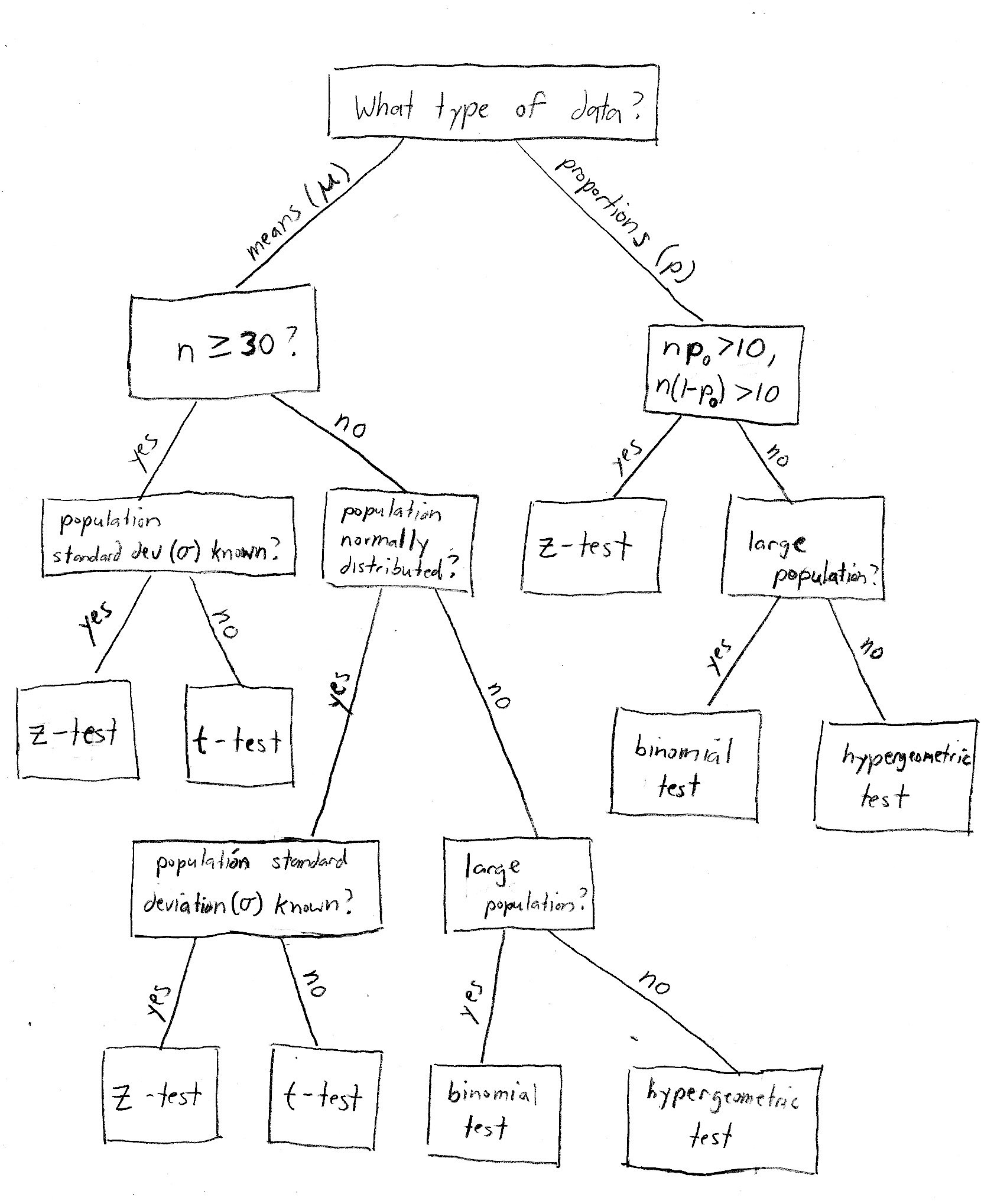
1. 检验的分类
对于检验来讲,有着不同的分类方法。
比如按照样本数分类,可以分为单样本检验,双样本检验,成对样本检验等。
比如按照检验的对象,可以分为对均值的检验,对方差的检验,对比例的检验等。
比如按照总体分布来区分,可以分为对正态总体做检验,对伯努利分布做检验等,或者在总体分布未知的情况下的检验。
对于不同的问题,要使用不同的检验方法。在R语言的stats package中,提供了多达33种不同的检验方法。使用lsf.str("package:stats")可以查看stats中的函数,这里对其中的部分检验方法简单介绍下:
ansari.test,Ansari–Bradley检验, 对双样本的标准差的区别检验。\(\gamma = Var(x) / Var(Y)\),零假设是\(\gamma\)等于1bartlett.test,Bartlett检验,检验是否k个样本有相同的标准差。binom.test,伯努利检验,用在很多的情况下,最常用的是检验两组样本发生概率是否相同(比如硬币的正反面)。特别用在关于比例的检验上,很多问题都可以归约成伯努利检验。Box.test,Ljung–Box检验,用来检测一组时间序列的自相关函数是否与0不同,它根据多个滞后时间来测试总体的随机性。chisq.test,卡方检验\(\chi^2 \; test\),也是一个很重要的检验手段,用在很多方面。比如根据频率检测两组样本是否相互独立;或者检验原分布是否为卡方分布。cor.test, 相关性测试,对成对样本的相关性的测试,可以使用多种测试方法。fisher.test,Fisher精确检验,用来检验一个table中行和列是否相互独立。fligner.test,Fligner Killeen检验,用于检验两组分布方差是否相同。friedman.test,quade.test略kruskal.test,Kruskal-Wallis检验,在不假设总体分布的情况下,检验它们是否相互独立。ks.test,Kolmogorov–Smirnov检验,用来检验两个数据是否显著不同,ks检验是非参数检验,不需要指定样本的分布。它可以是单样本(与参考概率分布相比较),也可以是双样本。mood.test, Mood’s Median检验,属于非参数检验,基本上是符号检验(Sign Test)的双样本或多样本版本,用在检测两个独立样本的中值是否相等。oneway.test, 也叫one-way ANOVA,用来分析来自正态分布的两个或多个样本的均值是否相当(不需要知道方差)poisson.test, possion检验,对possion分布里的比例参数做假设检验。prop.test,用来检验几组样本中,成功的概率(或比例)是否相同。或者有特定值相同。shapiro.test,Shapiro–Wilk检验,用来判断样本是否为正态分布。t.test,t检验,几乎是最重要也是最常用的检验,常用在检验样本均值。当标准差已知的时候,会使用z检验。wilcox.test,Wilcoxon符号秩检验。常用的非参数统计假设检验,和t检验类似。但当原分布未知的时候使用。
这里用一张图,来说明一下常用的检验的一般流程。
2. 几种常用的传统检验
这里的例子都引自吴喜之老师的书<统计学:从数据到结论>。
2.1 对于正态均值的检验
2.1.1 单样本正态均值检验
监管部门称了50包标有500g重的红糖,均值为498.35g,少于500g。
由均值,怀疑是否够分量,这里就可以做统计检验。因为厂家声称每袋重500g,因此零假设为总体均值等于500g。正好是我们要检验的内容。因为怀疑每袋的重量小于500g,所以备选假设定为总体均值小于500g。(也就是单侧检验,这里是left tailed)
- \(H_0: \; \mu = 500\)
- \(H_1: \; \mu < 500\)
这里的样本量比较大,但总体均值未知。因此使用t检验。
x = scan("sugar.txt")
t.test(x, mu = 500, alternative = "less")##
## One Sample t-test
##
## data: x
## t = -2.6962, df = 49, p-value = 0.004793
## alternative hypothesis: true mean is less than 500
## 95 percent confidence interval:
## -Inf 499.3749
## sample estimates:
## mean of x
## 498.3472这里t值为\(-2.6962\),而p值为\(0.004793\),如果选择显著性水平(\(\alpha\))为0.005,那么拒绝错误的概率为0.005。这是个很小的概率,属于小概率事件。
对于这个例子来说,也就是说,认为产品均值小于500g犯错的概率为0.005,也就是说认为产品均值小于500g基本上是没错的。
在图中看一下t值的位置: 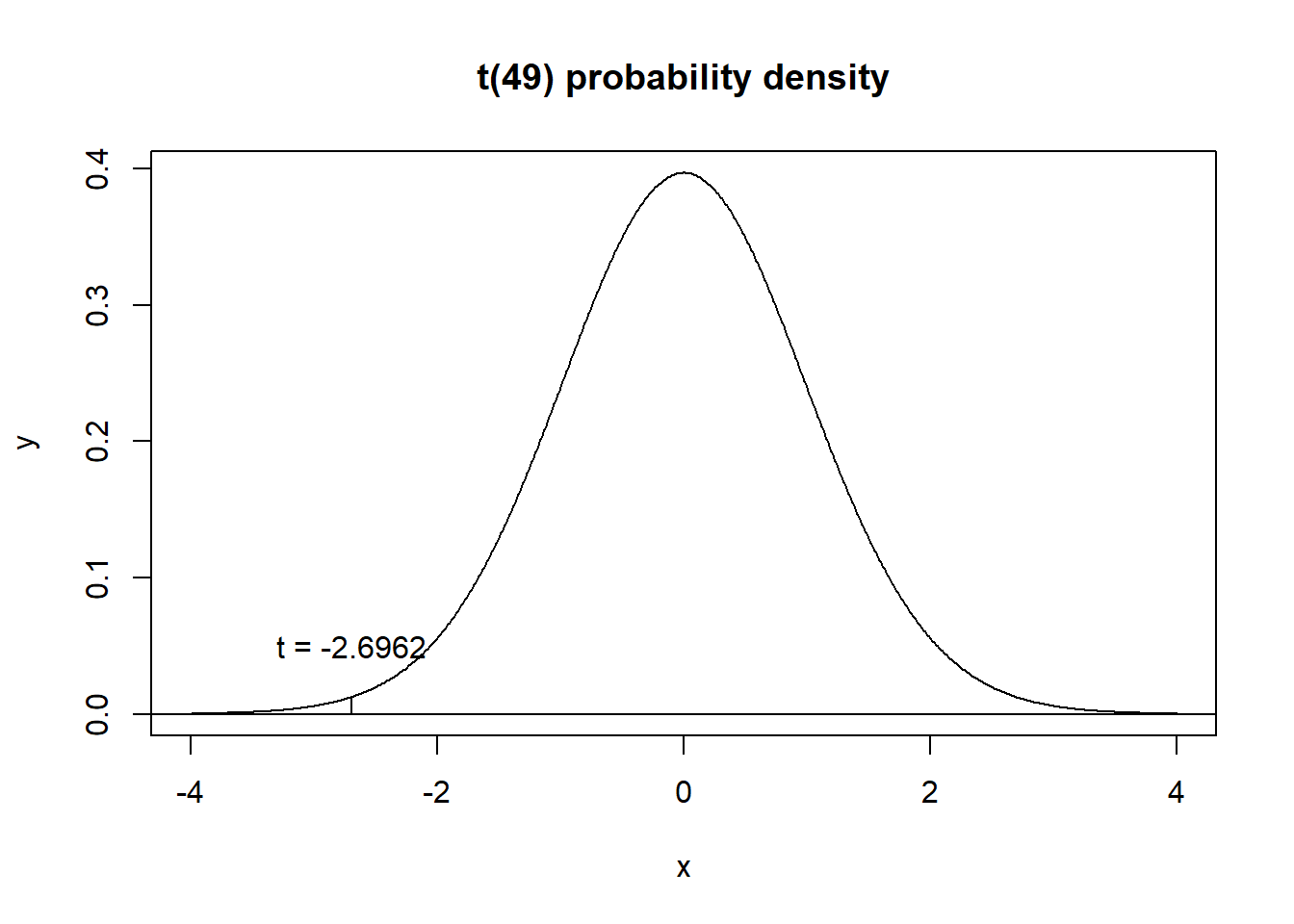
可以看出来,t统计量取值在一个非常小概率的位置。左侧尾概率是一个小概率。
2.1.2 检验区间
上一个例子中,采用了单尾检验(left tailed)。这是因为这个问题只关心小于的部分。实际中,可以根据大于,小于,不等于三个问题把检验分为三种情况:
- 备选假设为小于,那么选择左侧检验(left tailed test)
- 备选假设为大于,那么选择右侧检验(right tailed test)
- 备选假设不等于,那么选择双侧检验(two tailed test)
2.1.3 双样本正态均值检验
为检验某种药物的影响,对处理组的100名人员和对照组的150名人员检验某种指标。
对这个问题中指标的检验,就相当于是双样本的正态均值检验。比如问题是处理组的总体均值\(\mu_1\)是否大于对照组的总体均值\(\mu_2\)。
- \(H_0: \; \mu_1 = \mu_2\)
- \(H_1: \; \mu > \mu_2\)
或者也可以写成:
- \(H_0: \; \mu_1 - \mu_2 = 0\)
- \(H_1: \; \mu_1 - \mu_2 > 0\)
dt = read.table("drug.txt", header = T)
x = dt[dt$X1==1,1]
y = dt[dt$X1==2,1]
t.test(x, y, alternative = "greater")##
## Welch Two Sample t-test
##
## data: x and y
## t = 0.94456, df = 231.72, p-value = 0.1729
## alternative hypothesis: true difference in means is greater than 0
## 95 percent confidence interval:
## -0.3742108 Inf
## sample estimates:
## mean of x mean of y
## 8.60202 8.10200可以看出,结果中,p值为0.1729,不能明显拒绝两个均值相等的零假设。
2.1.4 成对样本的检验
例如给出50个人减肥前和减肥后的体重。这样的数据就属于成对样本。如果使用t.test(x, y, alternative = "greater")这样的检验就不行,因为x和y并不是相互独立的。很显然,减肥前体重和减肥后的体重是相关的。因此如果这样计算就会得到错误的结果。
实际上应该利用每个人是相互独立的,来得到单样本进行计算。即用减肥后的体重减去减肥前的体重,对这一差值做检验: t.test(x-y, alternative = "greater").但这样检验实际上是对\(\mu=0\)做的比较。在R的检验里提供了成对样本的选项,可以更加方便地直接使用参数控制。
比如需要检验减肥前的体重大于减肥后的体重:
t.test(w$before, w$after, alternative = "greater", paired = TRUE)2.2 关于比例的检验
2.2.1 关于总体比例的检验
对某个电视节目,调查显示,被访问的1500人中有23%的收视率。现在想知道这是否和所期望的25%显著不足。
通过图可以看出,此处应该使用z检验。所谓z检验,指的是在n很大的情况下的大样本的正态近似。z值为\(z = \frac{\hat{p}-p_0}{\sqrt{\frac{p_0(1-P_0)}{n}}}\)。在R中使用的是prop.test,是在基于z值的修正下做的z检验。
但在计算机时代,完全不必要做这样的假设,可以直接做精确的计算。
对于这个问题,即伯努利检验,使用r中的binom.test:
binom.test(0.23*1500, 1500, p = 0.25, alternative = "less")##
## Exact binomial test
##
## data: 0.23 * 1500 and 1500
## number of successes = 345, number of trials = 1500, p-value =
## 0.03837
## alternative hypothesis: true probability of success is less than 0.25
## 95 percent confidence interval:
## 0.0000000 0.2485905
## sample estimates:
## probability of success
## 0.23如果选定\(\alpha\)为0.05,那么就有足够的理由拒绝零假设。即可以认为收视率小于25%。
2.2.2 关于总体比例的双样本检验
在binom.test中,如果是双样本的比较,那么可以用向量。比如对两个节目的收视率比较,调查观众1200人,A节目收视率为20%,调查观众1300人,B节目收视率为21%,是否可以认为A节目收视率比B节目低:
binom.test(c(0.2*1200, 0.21*1300), c(1200, 1300), alternative = "less")##
## Exact binomial test
##
## data: c(0.2 * 1200, 0.21 * 1300)
## number of successes = 240, number of trials = 513, p-value =
## 0.07882
## alternative hypothesis: true probability of success is less than 0.5
## 95 percent confidence interval:
## 0.0000000 0.5051157
## sample estimates:
## probability of success
## 0.46783633. 非参数检验
3.1 非参数检验的介绍
传统的检验方法都假定了背景的分布,基于已有的分布来判断样本概率。而非参数检验是指在样本背景分布未知的情况下做的判断。比如Fisher精确检验,连续变量比例的检验,pearson \(\chi^2\)检验和似然比\(\chi^2\)检验都属于非参数检验。
非参数检验中常用到的一个概念是秩(rank),秩指的是样本数据按照升幂排列之后,每个观测值的位置。比如:
\[ 15\;\;9\;\;18\;\;3\;\;17\;\;8\;\;5\;\;13\;\;7\;\;19\]
经过升幂排列后,为
\[3\;\;5\;\;7\;\;8\;\;9\;\;13\;\;15\;\;17\;\;18\;\;19\]
| 观测值 | 3 | 5 | 7 | 8 | 9 | 13 | 15 | 17 | 18 | 19 |
|---|---|---|---|---|---|---|---|---|---|---|
| 秩 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
如果有重复,就取平均,比如1,2,2,3。那么秩就为1,2.5,2.5,4。
3.2 单样本位置的符号检验
3.2.1 符号检验的示例
对某商店的西洋参进行抽查,对25包标有净重100g的西洋参片称重。怀疑其分量不足。
这个问题,就相当于对样本的中位数进行检验。如果是正态分布或者是t分布这样的对称分布,那么中位数就相当于是均值。这里类似的,做符号检验(sign test):
- \(H_0:\; m = 100\)
- \(H_1:\; m < 100\)
按照零假设,每个观测值小于100的概率都是50%。也就是服从二项分布:
x = scan("gs.txt")
# 方法一
pbinom(sum(x>100), 25, 0.5)## [1] 0.05387607# 或者是
binom.test(sum(x>100), 25, 0.5, alternative = "less")##
## Exact binomial test
##
## data: sum(x > 100) and 25
## number of successes = 8, number of trials = 25, p-value = 0.05388
## alternative hypothesis: true probability of success is less than 0.5
## 95 percent confidence interval:
## 0.0000000 0.5036416
## sample estimates:
## probability of success
## 0.32大于零假设中中位数\(m_0\)的值的个数等于所有观测值减去\(m_0\)所得符号为正的个数,而小于的则为符号为负的个数。因此称其为符号检验(sign test)
3.2.2 符号检验的一般流程
符号检验的一般流程是这样的。对于大小为n的样本,观测值为\(x_1,x_2,x_3...,x_n\),零假设为样本中位数等于某个值M。假设\(r^+\)表示观测值中大于M的值而\(r^-\)表示观测值中小于M的值,等于M的值可以忽略,那么\(r^+\)与\(r^-\)的和记作\(n'\)
零假设下,那么应该有\(r^+\)与\(r^-\)的值相等,遵循\(p=\frac{1}{2}\)的二项分布。
检验的流程:
- 选择\(r = max(r^+,r^-)\)
- 观测在r值的情况下,\(p=\frac{1}{2}\)的二项分布的概率。如果是单侧检验,那么这个值就是p值。如果是双侧检验,该值乘2即为p值。即在上一部分示例中的方法1。
3.3 Wilcoxon符号检验
3.3.1 单样本位置的Wilcoxon符号检验
可以看出,在符号检验中,仅用到了大于中位数和小于中位数的情况,而差的绝对值的秩的大小并没有使用。如果结合秩的大小,那么检验效果自然更加有效。也就是Wilcoxon符号秩检验(Wilcoxon signed-rank test)的宗旨。
Wilcoxon符号秩检验和符号检验的思路类似,只不过按照秩做了加权。做法如下:
对\(|x_i-m_0|\)做排序,然后把\(x_i-m_0\)的符号加到秩上面。 对带符号的秩求和,即得到\(W^-\)和\(W^+\),和符号检验中的么\(r^+\),\(r^-\)类似。
在R中,只需要使用wilcox.test即可。
3.3.2 双样本的Wilcoxon检验
Wilcoxon检验和t检验用法很类似。也可以用在检测两个未知分布的样本中位数是否相等。语法和t检验也相同:wilcox.test(x.y,alternative = "less")